Gröbner Basis-Attacking a Tiny Sponge
| 🛈 |
|---|
| I originally wrote this post when working at AS Discrete Mathematics as part of a project sponsored by the Ethereum Foundation. It is reproduced here with friendly permission. |
When estimating the security of a cipher or hash function, there are many different attack scenarios to consider. For Arithmetization Oriented Ciphers (AOCs), Gröbner basis attacks are a lot more threatening than they are to “traditional” ciphers, like the AES. The most common way to argue resistance against Gröbner basis attacks is to look at the expected complexity of Gröbner basis algorithms.
However, the complexity estimates only apply asymptotically, and the Big O notation might hide factors that are significant for parameter sizes a cipher designer is interested in. Thus, to validate whether the theoretical complexity estimates carry significance, we need “real” data to compare it to. This means running experiments – and that's exactly what this post is about. Concretely, we have performed several Gröbner basis attacks, and will be discussing and interpreting the resulting data here.
Disclaimer
Take below results with a grain of salt – the data might be wrong. As far as I know, no one has reproduced it yet. If you have run your own, comparable experiments, please let me know! Please draw any conclusions carefully.
Prerequisites
We assume a certain familiarity with the ciphers Rescue-Prime [4] and Poseidon [3], as well as the Sponge construction. As a quick reminder for these three things, there are graphical depictions at the end of this post and in the next section, respectively.
Since this post is all about Gröbner basis attacks, a certain familiarity on this topic does not hurt, albeit it shouldn't be strictly necessary. In case you want to brush up on a detail or two, have a look here.
Description of Experiments
AOCs like Rescue-Prime and Poseidon are designed to have a “small” algebraic description. That is, when polynomially modeling their structure, we don't need too many polynomials, and those are not of very high degree.
A use case where an AOC's simple algebraic description causes major speedups involves hashes in zero-knowledge proof systems. The most popular way to transform a permutation, like Rescue-Prime or Poseidon, into a hash function is the Sponge construction. On a high level, a Sponge looks like this:
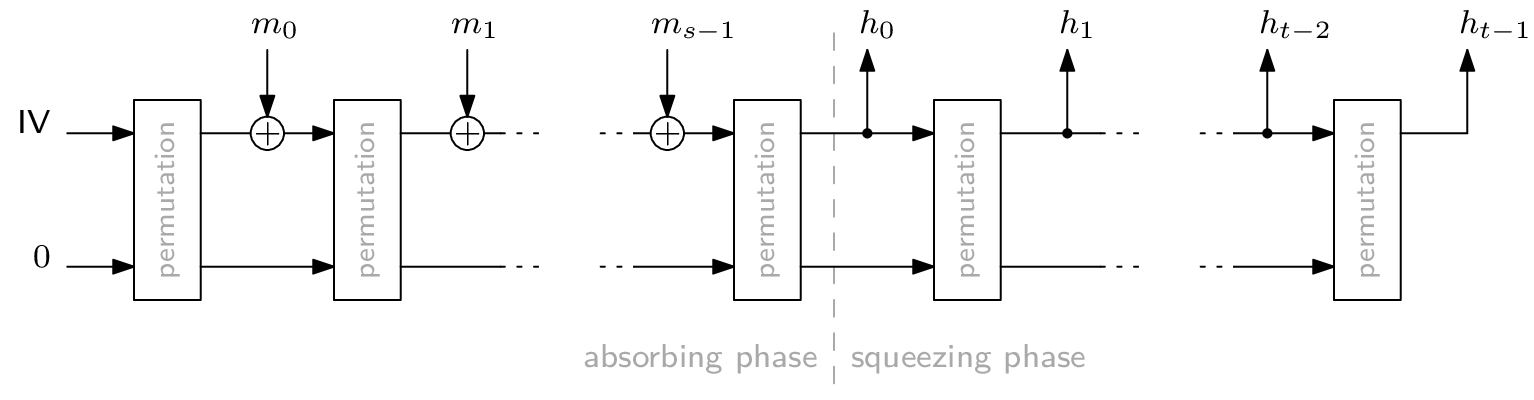
Any cryptographic hash function needs to be secure against inversion, i.e., computing a pre-image for a given hash digest must be so difficult as to be infeasible. For the Sponge construction, this largely depends on the plugged-in permutation. For our experiments, we perform a second pre-image Gröbner basis attack on a Sponge construction with exactly one application of the permutation. Furthermore, we set rate = capacity = 1, which is the lowest meaningful value for either parameter. This way, we get the smallest Sponge one can build. Consequently, if this attack is infeasible, then Gröbner basis attacking a realistically sized Sponge definitely is.
As the permutation, we use the two primitives Rescue-Prime and Poseidon with varying numbers of rounds. The prime field has size p = 65519, which is the largest 16-bit prime for which gcd(p-1, 3) = 1, meaning we can use exponent 3 in the S-Boxes. For the largest 16-bit prime, i.e., 65521, we'd have to use exponent 11. The limitation to 16-bit primes comes from the used Gröbner basis computation implementation, namely FGb [2].
Technical Specifications
All the experiments were performed using cocalc on an “n2-highmem-32 Cascade Lake Google Compute Engine” and 264141536 KiB (~252 GiB) of total RAM as reported by free.
The operating system in use was (Ubuntu) Linux 5.4.0-1042-gcp x86_64 as reported by uname -srm
Reproducibility
The code for the experiments can be found on github. Its dependencies are sagemath, fgb_sage, and FGb [2]. If you have the abilities and capacity to re-run the code to strengthen or refute the claims made here, I encourage you to do so.
Summary of Results
Before looking at the data in a little more detail, here's a quick summary of some of my findings.
- We managed to compute a Gröbner basis for 6 rounds of Rescue-Prime, but failed at 7 rounds.
- Poseidon has a two types of rounds, which makes arguing about round limits a little more cumbersome. With the exception of one outlier, we could not break any partition totaling 11 rounds – see the matrix below.
- Memory, not time, seems to be the most limiting factor.
- The polynomial system for Poseidon appears to be irregular, in contrast to the authors' implicit assumption. This directly affects the number of recommended rounds. For example, while Poseidon's authors recommend (8,9) rounds for p = 65519 and 2 elements in the state, extrapolating the data here suggests that (8,24) rounds might be necessary.
- The interpolation for the degree of regularity for Rescue-Prime is different from the interpolation published with Rescue, but similar in principle. This difference might be explained by the use of Rescue-Prime as the permutation. Sadly, it neither validates nor refutes the authors' claims.
Results in Detail
Experiments like the ones described above generate quite a bunch of data. We're not gonna look at everything here, I just want to highlight some parts. If you want to start digging deeper, you can find the raw data at the end of this post.
The metric commonly used to estimate the complexity of a Gröbner basis computation is largely depending on the degree of regularity. In this post, I will be using ”degree of regularity“ and “maximum degree reached by F4 during its execution” interchangeably. Indeed, it is an open question whether this is always true. This is not based on a totally rigorous argument, but it seems to be “good enough” in practice. Consequently, quite a bit of the following will be about the degree of regularity and the Macaulay bound. If you want to jog your memory on either of these concepts, I suggest taking a glance at this document. The Macaulay bound is an upper bound for the degree of regularity, and their values coincide if a polynomial system is a regular sequence.
In general, the successful attacks that took the longest time for the two primitives were 6-round Rescue-Prime, and (full=2, partial=9)-round Poseidon. They took around 34 and 73 hours, requiring roughly 75 and 228 GiB of memory, respectively.
Rescue-Prime
We successfully computed a Gröbner basis for 6-round Rescue-Prime, but ran out of memory during the computation for 7-round Rescue-Prime.
Degree of Regularity
The most important metric to consider is the growth of the degree of regularity as a function in the number of rounds. As we can see, the degree of regularity is pretty consistently 2 less than the Macaulay bound of the polynomials system for Rescue-Prime. The only exception happens at r = 2 rounds, an anomaly I don't believe deserves a lot of attention.
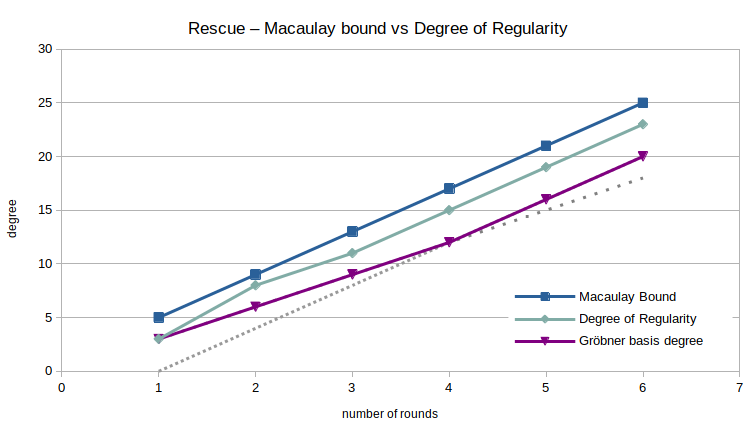
Interestingly, the degree of the highest degree polynomial in the resulting reduced Gröbner basis – abbreviated as the degree of the Gröbner basis – is even lower than that. More importantly though, its growth seems to be only piecewise linear: between 1 and 4 rounds, the degree of the Gröbner basis grows by 3 with each iteration, where from round 4 on, the difference is 4.
The limited number of data points makes drawing conclusions difficult. However, it's not unreasonable to argue that extrapolating the degree of the Gröbner basis linearly might lead to inaccuracies. Similarly, it is still an open question whether extrapolating the degree of regularity is a good method to estimate the complexity of computing the Gröbner basis for the full-round primitive.
The observed growth of the degree of regularity in Rescue-Prime is different from what is reported in the publication of “plain” Rescue. Concretely, I observe for Rescue-Prime, whereas Rescue's authors report for Rescue [1, Section 6.1]. Here is their figure for comparison:
Extending this interpolation of the degree of regularity to an extrapolation can be used to estimate the required number of rounds to achieve a given security level. For this, we use the known complexity bound for the most performant Gröbner basis algorithm, which is . Here, n is the number of variables in the polynomial ring, is the degree of regularity, and ω is the linear algebra constant. A conservative choice for ω is 2. I know of no Gröbner basis algorithm making use of sparse linear algebra techniques, which would imply ω = 2. However, it is plausible that they do or can exist. For the used parameters of Rescue-Prime, the number of variables, which is equal to the number of equations, is 2r. The degree of regularity is estimated to be 4r - 1. Putting it all together, we have for r ≥ 13. For the same parameters, the authors of Rescue-Prime recommend r = 27 [4, Algorithm 7]. This recommendation also includes a security margin, and considers more attack vectors than just a Gröbner basis attack.
F4's Working Degree
For Rescue-Prime, the working degree of F4 increases strictly monotonously: every iteration of F4's main loop means working with polynomials of degree exactly 1 higher than in the preceding iteration. That makes for a pretty dull figure:
Poseidon
Since Poseidon has two types of rounds, namely full rounds and partial rounds, we have conducted a lot more experiments for Poseidon than for Rescue. The following matrix summarizes which ones we ran, and whether the Gröbner basis could be computed successfully. The value of a cell indicates how many polynomials the polynomial system had. This is equal to the number of variables in the polynomial ring for this problem instance. The number of full rounds differ across columns, the number of partial rounds across rows.
| 2 | 4 | 6 | 8 | 10 | 12 | |
| 0 | 3 | 7 | 11 | 15 | 19 | 23 |
| 1 | 4 | 8 | 12 | 16 | 20 | |
| 2 | 5 | 9 | 13 | 17 | 21 | |
| 3 | 6 | 10 | 14 | 18 | ||
| 4 | 7 | 11 | 15 | 19 | ||
| 5 | 8 | 12 | 16 | |||
| 6 | 9 | 13 | 17 | |||
| 7 | 10 | 14 | ||||
| 8 | 11 | 15 | GB computed | |||
| 9 | 12 | 16 | out of memory | |||
| 10 | 13 | manually aborted | ||||
A total of 11 rounds seems to the barrier we couldn't break with the available machine, the (2,9)-instance being a notable exception. Note that the number of equations seems to not be the cutoff point – for (2,10)-Poseidon, we have 13 equations and variables but cannot compute the Gröbner basis, whereas for (10,0)-Poseidon with its 19 equations, we can compute the Gröbner basis. For some of the figures below, we look at the series for full rounds in more detail to simplify presentation.
Degree of Regularity
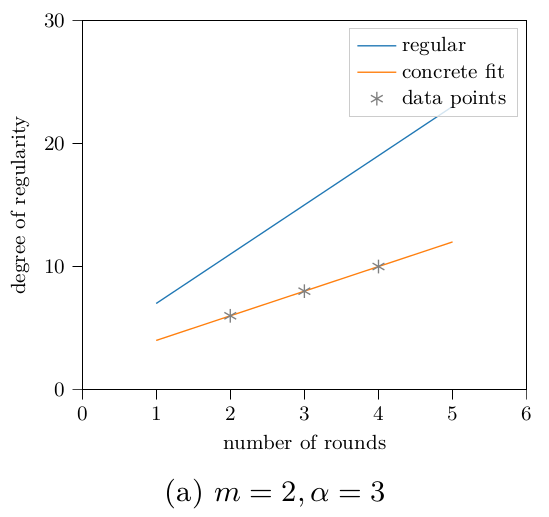
As before, the degree of regularity is the metric we're interested in the most. For example, for Poseidon (4,٭), i.e., 4 full rounds and a varying number of partial rounds, we get the following figure when plotting both the Macaulay bound and the system's degree of regularity.
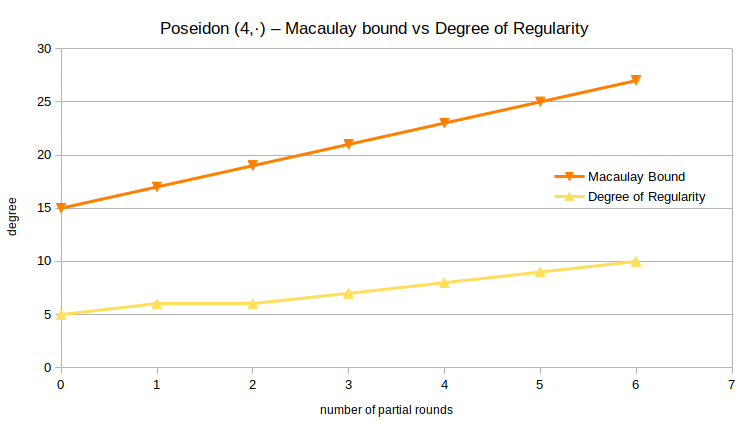
It appears the degree of regularity is growing slower than the Macaulay bound. For a more complete picture, the degrees of regularity for all successfully computed Gröbner bases are listed in the following table. A grayed-out value means that the Gröbner basis computation did not terminate, but reached the indicated degree at its maximum before running out of memory or being aborted manually.
| 2 | 4 | 6 | 8 | 10 | 12 | |
| 0 | 4 | 5 | 6 | 7 | 8 | 8 |
| 1 | 5 | 6 | 6 | 7 | 8 | |
| 2 | 5 | 6 | 7 | 8 | 8 | |
| 3 | 6 | 7 | 8 | 9 | ||
| 4 | 7 | 8 | 9 | 9 | ||
| 5 | 8 | 9 | 9 | |||
| 6 | 9 | 10 | 10 | |||
| 7 | 10 | 11 | ||||
| 8 | 11 | 12 | ||||
| 9 | 12 | 13 | ||||
| 10 | 13 |
We can compute the Macaulay bound for the polynomial system arising from -Poseidon as . A closely fitting linear approximation for the degree of regularity based on above data is . The (limited) data suggests that the degree of regularity depends on a full round a lot less than the Macaulay bound makes it seem. Overall, the degree of regularity does not stay very close to the Macaulay bound.
Based on the script supplied by the authors of Poseidon, the recommended number of rounds for 128 bits of security when using a state size of 2 is (8, 9). Using the number of full rounds as a given, and plugging the interpolated degree of regularity, i.e., r + 6, and the required number of variables, i.e., r + 15, into the complexity bound for the most performant Gröbner basis algorithm leads us to the conclusion that r ≥ 24 partial rounds are necessary to achieve 128 bits of security against Gröbner basis attacks, i.e., for r ≥ 24. This discrepancy is the direct consequence of the observed degree of regularity not equaling the Macaulay bound – plugging the Macaulay bound into the same formula results in r ≥ 10.
F4's Working Degree
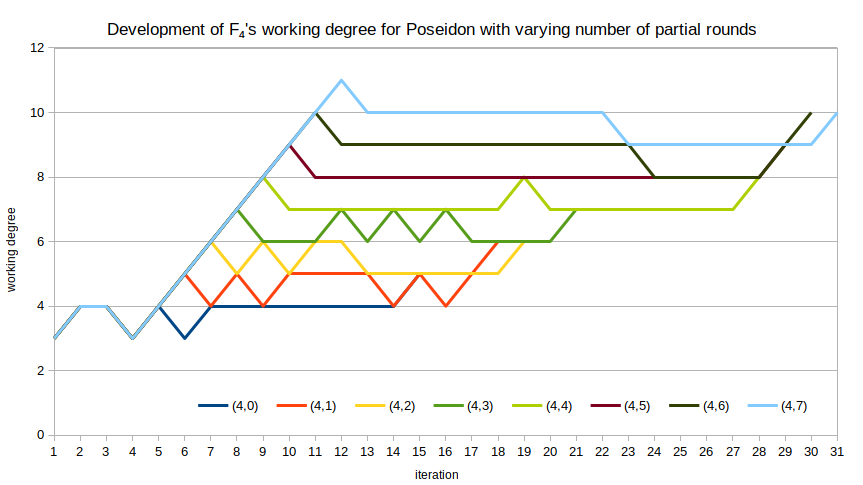
The working degree of F4 is quite “bouncy” for the polynomial systems derived from Poseidon. For example, for with varying number of partial rounds, we can plot the working degree of F4 against the iteration that degree occurred in. While the overall tendency is “up,” there are many iterations for which the working degree does not change, or even drops. I am unsure what exactly this means in terms of security, or if it means anything at all.
Comparison: Rescue-Prime vs Poseidon
One of the most notable differences between the polynomial systems for Rescue-Prime and Poseidon is the growth rate of their respective degrees of regularity. For example, consider the following plot, where I have repeated the data for Rescue-Prime from above and added the Macaulay bound and degree of regularity for (٭,0)-Poseidon, i.e., varying the number of full rounds.
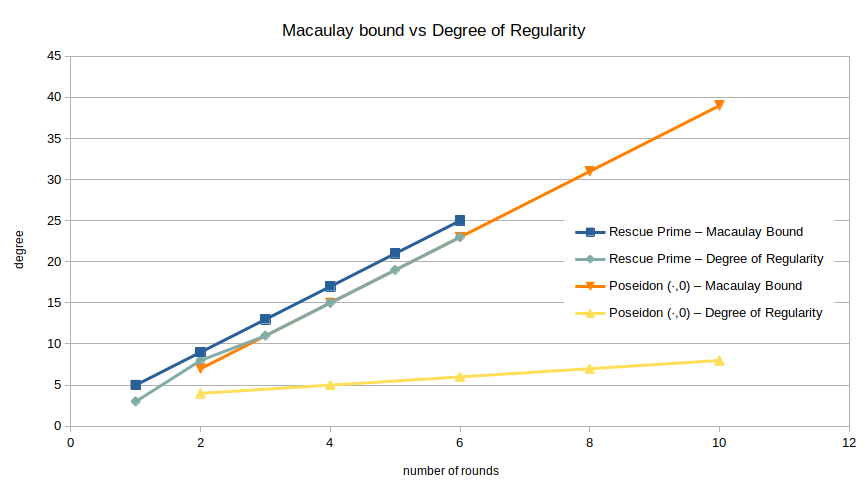
While the Macaulay bounds are almost identical, the observed degrees of regularity differ greatly.
It's also nice to see the development of the used memory for a few instances, even though that comparison is not very important. Below figure shows the required memory over time for 5, 6, and 7-round Rescue-Prime and (4,5), (4,6), (4,7)-round Poseidon. Recall that 7-round Rescue-Prime and (4,7)-round Poseidon both ran out of memory, i.e., terminated abnormally.
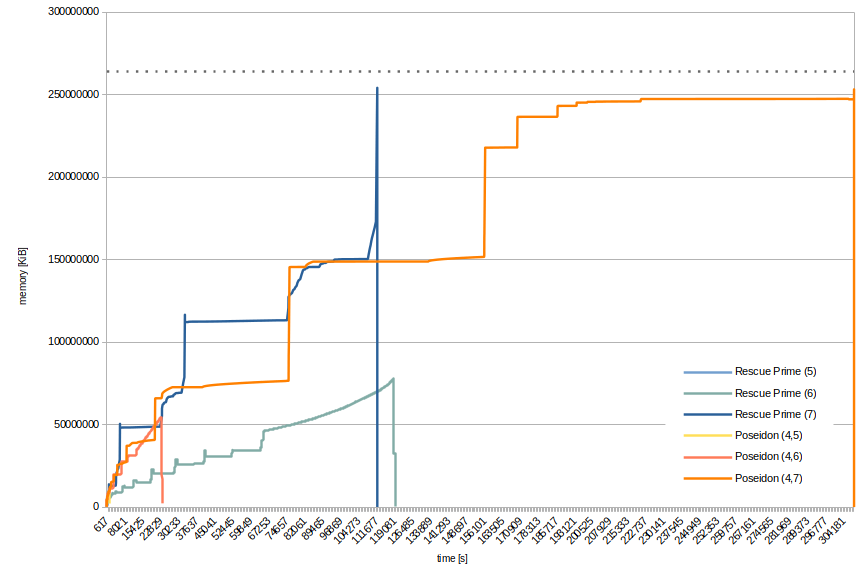
By the jumps in memory consumption you can pretty clearly see where a new, bigger matrix was constructed. This corresponds to the iterations of F4. Exponential – or binomial – growth being what it is, it does not make sense to plot instances with less rounds. Already, 5-round Rescue-Prime and (4,5)-round Poseidon are barely visible in the lower-left corner of the figure. The dotted line corresponds to the total available memory.
Conclusion
The data suggests that the implicit assumption about the regularity of the polynomial system arising from Poseidon is wrong: the difference between the Macaulay bound and the observed degree of regularity implies that the system is irregular. This has direct consequences for the minimum number of rounds required to achieve a target security level. For example, for p = 65519 and state size 2, we recommend (8,24) rounds as opposed to (8,9) rounds.
An interesting open question is how to interpret the “bounciness” of F4's working degree when computing a Gröbner basis for a Poseidon-derived system. The significance of this behavior is completely unclear.
Another open question regards the discrepancy in the observed growth of the degree of regularity for Rescue and Rescue-Prime. Regardless, the data supports the security argument of Rescue-Prime: adding one half round at either end, i.e., transforming “plain” Rescue into Rescue-Prime, does not seem to decrease security.
All things told, no successful Gröbner basis attack could be performed for anything approaching realistic round numbers – even for this tiny Sponge construction.
References
- Aly, A., Ashur, T., Ben-Sasson, E., Dhooghe, S., Szepieniec, A.: Design of Symmetric Primitives for Advanced Cryptographic Protocols. IACR ToSC 2020(3), 1–45 (2020)
- J.-C. Faugère: FGb: A Library for Computing Gröbner Bases. In Komei Fukuda, Joris Hoeven, Michael Joswig, and Nobuki Takayama, editors, Mathematical Software ICMS 2010, volume 6327 of Lecture Notes in Computer Science, pages 84-87, Berlin, Heidelberg, September 2010. Springer Berlin / Heidelberg.
- Grassi, L., Khovratovich, D., Rechberger, C., Roy, A., Schofnegger, M.: Poseidon: A New Hash Function for Zero-Knowledge Proof Systems. In: USENIX Security. USENIX Association (2020)
- Szepieniec, A., Ashur, T., Dhooghe, S.: Rescue-Prime: a Standard Specification (SoK). Cryptology ePrint Archive, Report 2020/1143 (2020)
Appendix – Summary of the Hash Functions
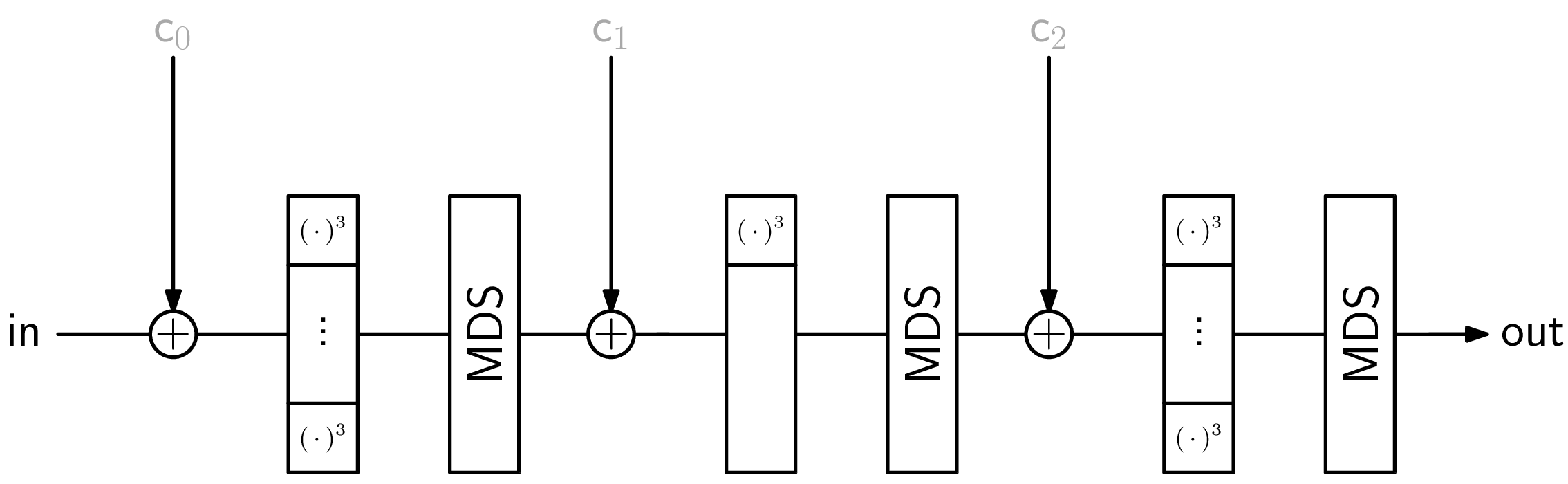
Below, I have put some figures summarizing the AOCs Rescue-Prime and Poseidon, respectively. The input, output, and constants are all vectors of the same length. They are contracted here to simplify presentation.

Appendix – Raw Data
Here's the data this post is based on! Each experiment, say, (4,3)-Poseidon, comes with 4 files: Yes, there are spaces in the filename. 🤦 Sorry.
poseidon_65519_(4, 3)_fgb_debug.txt- debug information of FGb, described on page 12 in this document.
poseidon_65519_(4, 3)_mem.txt- memory requirements over time, in KiB, one row per second.
poseidon_65519_(4, 3)_summary.txt- includes time & memory measurements, degrees, data from FGb.
poseidon_65519_(4, 3)_sys.txt- the polynomial system for which the Gröbner basis was computed.