Converting Gröbner bases with FGLM

Have you ever computed a Gröbner basis in some monomial order $\prec_0$ only to then realize that you actually wanted it in another order $\prec_1$ ? I know, happens all the time… But fret not, FGLM can convert between the two orders, and you don't have to start your computation from scratch.

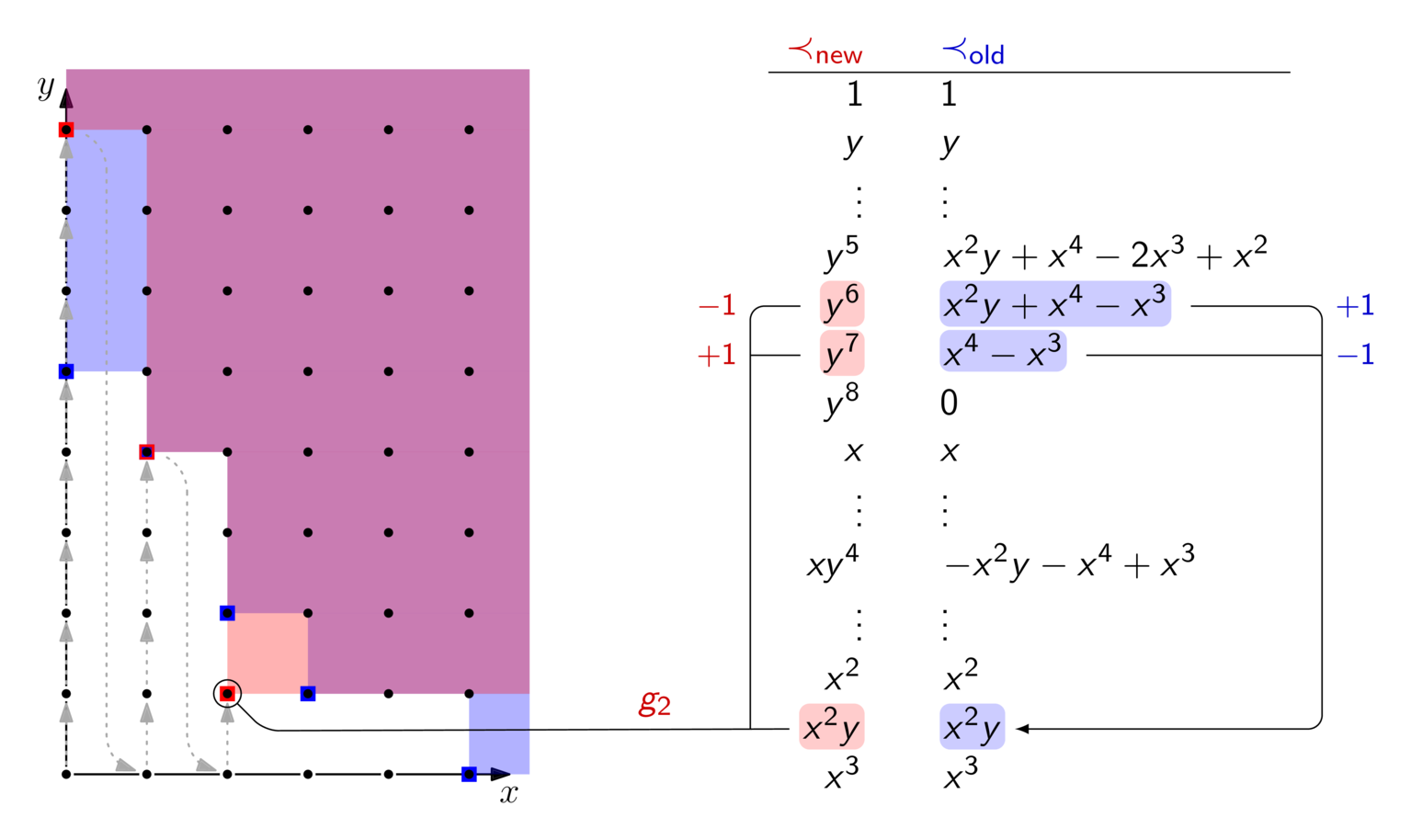
Here's a recording where I'm explaining how FGLM works. If you'd like to look through the slides at your own pace, here they are. You can also find the two Gröbner bases used in the example as well as pseudocode for FGLM in the slides, in case you want to retrace the steps yourself.

If you are interested in not only how but also why FGLM works, have a look at the original publication. Section 5 and 6 give a comprehensive overview of FGLM's complexity, which can be summarized as $O(n\cdot D^3)$ where $D$ is the dimension of quotient ring $k[x_0, \dots, x_{n-1}] / \langle G \rangle$ as a $k$ -vector-space. More intuitively, $D$ is the number of monomials in the staircase of a Gröbner basis, which are those dots in the non-blue region in this post's first picture.

def FGLM(order_new, gb_old, order_old):
    d = {}
    gb_new = []
    next_monoms = [1]
    while next_monoms:
        monom = min(next_monoms) # according to order_new
        next_monoms -= monom
        if no g in gb_new such that LM(g) | monom:
            # monom is still within staircase
            reduced_monom = monom.reduce(gb_old, order_old)
            if reduced_monom + sum([w[u] * v for u, v in d.items()]) == 0 for some w:
                # w[i] are field elements, i.e., coefficients.
                # they can be found by Gaussian reduction of d.values()
                gb_new += monom + sum([w[u] * u for u, v in d.items()])
            else:
                d += {monom : reduced_monom}
                next_monoms += [x_i * monom for i in range(n)]
    return gb_new